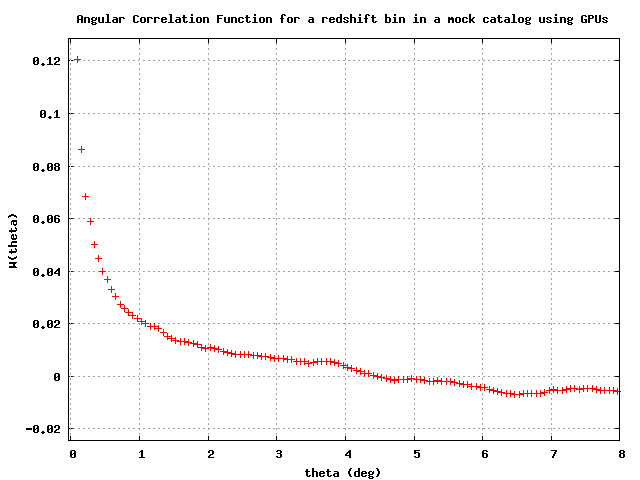
GP2PCF Abstract
The two-point correlation function is a simple statistic that quantifies the clustering of a given distribution of objects. In studies of the large scale structure of the Universe, it is an important tool containing information about the matter clustering and the evolution of the Universe at different cosmological epochs. A classical application of this statistic is the galaxy-galaxy correlation function to find constraints on the parameter Omega_m or the location of the baryonic acoustic oscillation peak. This calculation, however is very expensive in terms of computer power and Graphics Processing Units provide one solution for efficient analysis of the increasingly larger galaxy surveys that are currently taking place.
In this website we present a public code in CUDA to perform this computation, noting that with a single GPU board it is possible to achieve 120-fold speedups with respect to a standard implementation in C running on a single CPU. With respect to other solutions such as k-trees the improvement is of a factor of a few retaining full precision. The speedup is comparable to running in parallel in a cluster of O(100) cores.
GP2SSCF Abstract
Light rays are deflected when travelling through a gravitational potential, this phenomenon is known as gravitational lensing. This causes the observed shapes of galaxies to be distorted, the shape distortion is being called shear. For the vast majority of the galaxies this distortion is very small. By measuring this shear component it is possible to derive the mass distribution in the Universe, regardless of its nature: baryonic or dark matter. This in turn can lead to the measurement of the accelerated expansion of the Universe.
However, shear calculation requires the statistical analysis of the ellipticities of thousands of galaxies in very large astronomical surveys. In the past, due to the computational cost of the problem, this kind of analysis has been performed by introducing simplifications in data analysis in order to reduce its computational cost. With the advent of GPU processing, the shear analysis without approximations can be addressed, even for very large surveys, while maintaining an affordable execution time. In this work, the creation and optimization of such a code analysing shear-shear correlation is presented. |